前面文章中，我们提及了 peano 数类型：Nat，并且展示了隐式转换这项 Scala 黑科技的应用。

本文我们通过 HList 的 at 方法来进一步说明 Nat 类型和以及隐式转换在 shapeless 中的广泛应用

HList 的 at 操作

前文中提到： HList 可以看成是一个有各种类型连接而成的 List，如

1
2
type Foo = Int :: String :: Boolean :: HNil
val foo: Foo = 1 :: a :: true :: HNil

HList 有一个 at 函数

1
2
3
4
5
6
7
8
9
10
11
12
scala> foo.at(0)
res4: Int = 1

scala> foo.at(1)
res5: String = a

scala> foo.at(2)
res6: Boolean = true

scala> foo.at(3)
<console>:16: error: Implicit not found: shapeless.Ops.At[shapeless.::[Int,shapeless.::[String,shapeless.::[Boolean,shapeless.HNil]]], shapeless.Succ[shapeless.Succ[shapeless.Succ[shapeless._0]]]]. You requested to access an element at the position shapeless.Succ[shapeless.Succ[shapeless.Succ[shapeless._0]]], but the HList shapeless.::[Int,shapeless.::[String,shapeless.::[Boolean,shapeless.HNil]]] is too short.
       foo(3)

可以看到这个方法，能返回正确的类型而不是 Any，并且能在编译时做越界检查。

该如何实现这样的at方法？

1
def at(n: Int): X

首先我们想到的是用类型参数实现

1
def at[A](n: Int): A

然而调用时，仍旧需要手工指定 A 的类型。
同时，不用类型参数的前提下，一个方法又只能返回一种类型

下面我们介绍一种使用带抽象类型成员 typeclass 来解决返回不同类型的套路

实现基于 Nat 的 at 函数

为了简化问题，先用 Nat 代替 Int 表示元素所在的位置

1
def at(n: Nat): X

为了实现这个函数，我们先介绍一个套路:

如果一个类型 O 由其他几个类型 I1, I2,.. In 决定

那么我们可以构造一个 X[I1, I2, .., In] { type Out = O} 这样的 typeclass 用来计算出 O 对应类型

套用到上面的方法：HList 本身类型和元素所在位置 n，可以决定返回类型，我们可以得到以下定义

1
2
3
4
5
6
7
8
9

trait At[L <: HList, N <: Nat] {
  type Out
  def apply(l: L): Out
}

implicit class HListSyntax[L <: HList](l: L) {
    def at(n: Nat)(implicit at: At[L, n.N]): at.Out = at.apply(l)
}

at

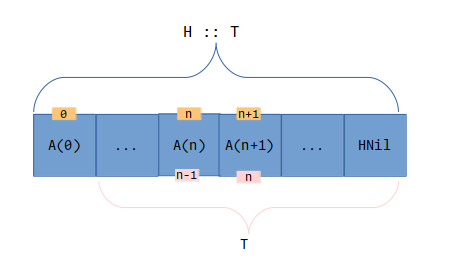
观察上图不难发现 T 的第 n 个元素类型就是 H :: T 的第 n + 1 个元素类型，即

1
2
3
4
5
// At[T, N] => At[H :: T, Succ[N]]
implicit def atN[H, T <: HList, N <: Nat](implicit att: At[L, N]): At[H :: L, Succ[N]] = new At[H :: L, Succ[N]]{
  type Out = att.Out
  def apply(h: H :: T) = att.apply(h.tail)
}

而第 0 个元素类型则显而易见的就是 head 的类型 H

1
2
3
4
implicit def atZero[H, T <: HList] = new At[H :: L, _0] {
  type Out = H
  def apply(l: H :: T) = l.head
}

由以上两条规则，则可以递归获得任意位置 n 上的元素类型

用 Aux 解决编译期类型丢失问题

然而，当我们尝试使用上述定义的 at 时会发生编译错误，告诉我们 Out 类型需要 ClassTag
这是因为编译器没法在编译时获得抽象类型成员 Out 的类型导致的

这里需要再一次使用 Aux 套路解决问题

最终我们得到如下定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
trait At[L <: HList, N <: Nat] {
  type Out
  def apply(l: L): Out
}

object At {
  type Aux[L <: HList, N <: Nat, O] = At[L, N] {type Out = O}
}

implicit class HListSyntax[L <: HList](l: L) {

  def ::[H] (h: H): (H :: L) = new ::(h, l)

  def at(n: Nat)(implicit at: At[L, n.N]): at.Out = {
    at.apply(l)
  }
}

implicit def atZero[H, T <: HList]: At.Aux[H :: T, _0, H] = new At[H :: T, _0] {
  type Out = H
  def apply(l : H :: T) = l.head
}

implicit def atN[H, T <: HList, N <: Nat](implicit at: At[T, N]): At.Aux[H :: T, Succ[N], at.Out] = new At[H :: T, Succ[N]] {
  type Out = at.Out
  def apply(l : H :: T) = at.apply(l.tail)
}

完整可执行代码可以参考 scasite 链接

从 Int 到 Nat

Shapeless 除了支持根据 Nat 类型获得对应元素外，还直接支持根据 Int 作为元素位置获取元素。
但 Scala 的 Int 目前不支持 literal singleton type，并且不存在可以递归推导的后继关系。
所以 shapeless 实际上是使用 macro 强行构造 Nat 实例来实现 Int -> Nat 的转换。由于实现较为简单，不再赘述。

总结

通过本文和前两篇文章，我们意识到 implicit 和递归推理的套路是 shapeless 实现泛型编程的基本调性。
后续文章不再重复阐述 shapless 的实现机制，转而着重介绍一些 shapeless 的实际应用